モデルの拡大・縮小、平行・回転移動を行う変換をいいます。
平行移動
\begin{align}
T =
\begin{bmatrix}
1 & 0 & 0 & T_x \\
0 & 1 & 0 & T_y \\
0 & 0 & 1 & T_z \\
\end{bmatrix}
\end{align}
回転
\begin{align}
R_x =
\begin{bmatrix}
1 & 0 & 0 \\
0 & cosα & -sinα \\
0 & sinα & cosα \\
\end{bmatrix}
\end{align}
\begin{align}
R_y =
\begin{bmatrix}
cosβ & 0 & sinβ \\
0 & 1 & 0 \\
-sinβ & 0 & cosβ \\
\end{bmatrix}
\end{align}
\begin{align}
R_z =
\begin{bmatrix}
cosγ & -sinγ & 0 \\
sinγ & cosγ & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\end{align}
スケール
\begin{align}
S =
\begin{bmatrix}
S_x & 0 & 0 \\
0 & S_y & 0 \\
0 & 0 & S_z \\
\end{bmatrix}
\end{align}
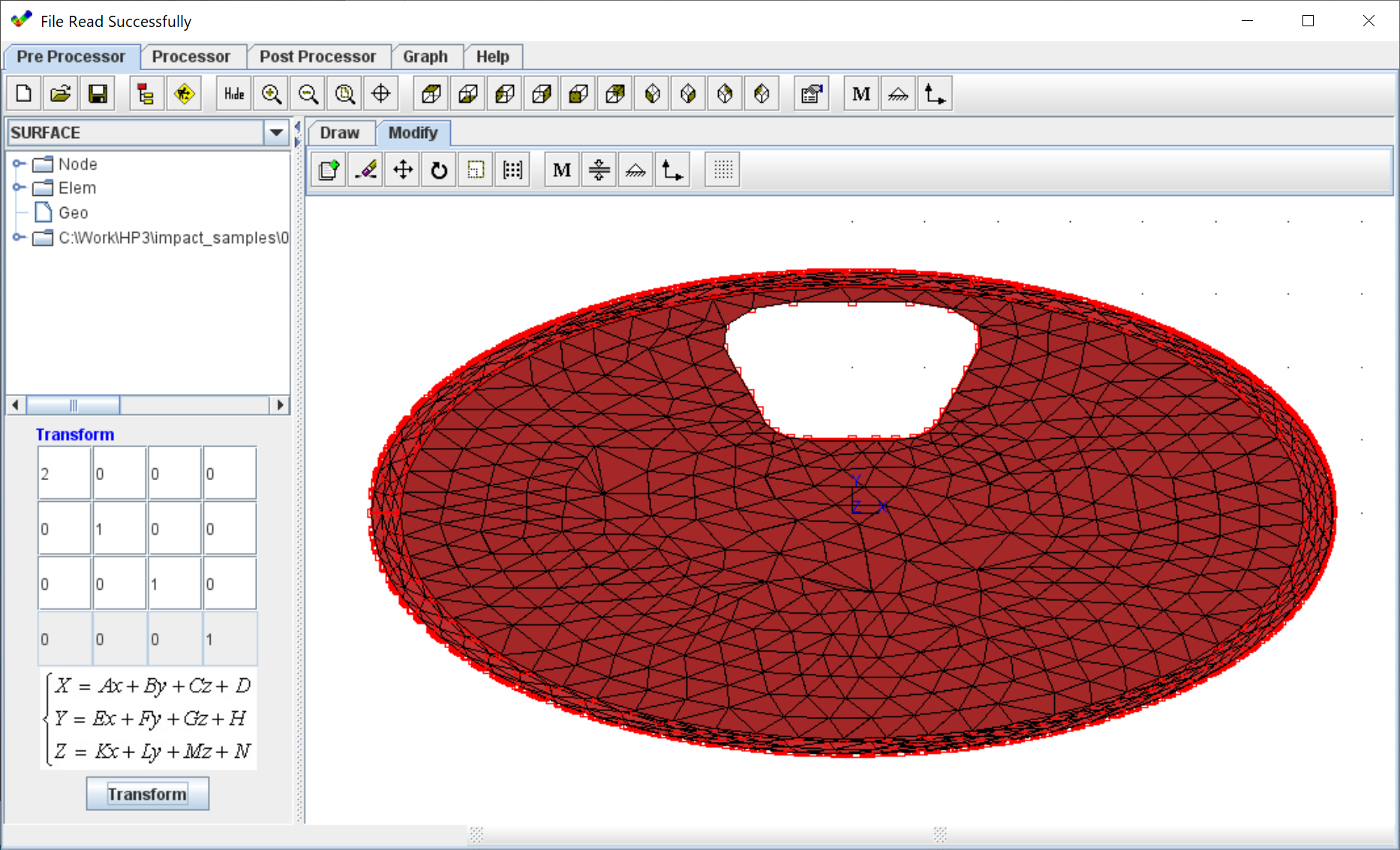
コメント